代表的な物価指数として、企業間で取引される時の財・サービスの価格を対象とした企業物価指数や家計が購入する財・サービスの価格を対象とした消費者物価指数などがあります。
企業物価指数の変動は、産業全体の経済活動に大きな影響を与えます。また、国民生活向上という視点からは、消費者物価指数が重要です。家計の生活水準が向上するかどうかは、賃金がどの程度の購買力を持つかにかかっていますから、賃金を消費者物価指数で除してもとめた実質賃金の動向に注目する必要があります。
産業連関分析でコアとなる価格は、産業別の「生産者価格」です。産業別生産者価格の変動が産業全体の経済活動に波及し、産業別生産者価格が消費者物価指数を形成して、国民生活に影響を与えます。
今回は、産業別生産者価格を考慮した産業連関表(3分類)をもとに、産業別生産者価格の決定要因とそれが産業全体にどのように波及するかをいくつかの事例をあげて論じます。さらに、国民経済に大きな影響を与える消費者物価指数は、どのようにして産業別生産者価格から形成されるかを説明します。
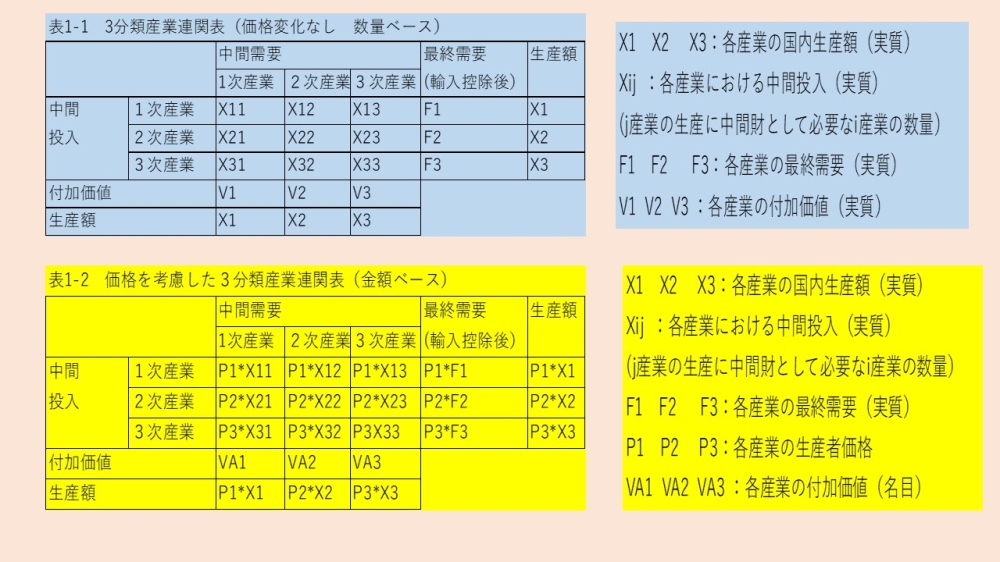
前回の投稿(注1)で用いた産業連関表は、価格は表面に出てこず、価格を考慮していませんでした。ところが、産業連関表は金額ベースで示されています。金額ベースとは、「価格×数量」ということですから、金額ベースの場合は価格を考慮するということになります。他方、前回の投稿のように価格を考慮しない場合は、数量ベース(=あるいは「実質ベース」)ということになります(表1-1参照)。
表1-2は価格を考慮した3分類産業連関表の事例を示しています。例えば1次産業で生産された財・サービスはP1で販売されます。この時、表1-2を行(=横)でみると、1次産業の財・サービスは、1次産業、2次産業、3次産業に中間財として、それぞれX11、X12、X13だけ購入されますから、「P1*X11+P1*X12+P1*X13」が金額ベースでみた中間需要になります。さらに、数量ベースの最終需要(輸入控除後)にP1をかけた「P1*F1」が金額ベースの最終需要(輸入控除後)となります。金額ベースの合計した需要(=中間需要+最終需要(輸入控除後))に等しく金額ベースの国内生産額「P1*X1」が決まることになります。2次産業、3次産業についても同様に考えることができます。
表1-2を列(=縦)でみた場合、供給構造あるいは費用構造を示します。例えば、1次産業は、「P1* X1」を生産すために、中間投入として「P1* X11+P2* X21+P3* X31」の費用を、労働や資本ストックの投入に対する対価である付加価値に「VA1」だけの費用を要したことがわかります。これらのことを各産業について式で表記すると、以下のような連立方程式になります。
P1*X11+P2*X21+P3*X31+VA1=P1*X1
P1*X12+P2*X22+P3*X32+VA2=P2*X2
P1*X13+P2*X23+P3*X33+VA3=P3*X3

「VA1/X1」、「VA2/X2」、「VA3/X3」が何かということですが、これらは各産業の1単位の生産に要した付加価値に係る費用を示します(=「単位あたり付加価値コスト」と便宜的に呼びます)。各産業の単位当たり付加価値コストはどのような要因で決まるかを考えてみます。
まず、VA1、VA2、VA3は各産業の付加価値で、定式化すると次式で示されます。
付加価値=雇用者所得+営業余剰
+固定資本減耗+間接税−補助金
尚、ここでいう付加価値は、固定資本減耗含む粗付加価値であることに留意して下さい。
営業余剰と固定資本減耗は、企業の取り分ですから、これらをまとめて「粗利潤」と呼ぶことにします。間接税から補助金をひいたものは「純間接税」と呼ばれ、政府の取り分になります。雇用者所得はいうまでもなく家計の取り分です。
粗利潤及び純間接税が名目国内生産額に占める割合を、それぞれ粗利潤率、純間接税率と呼ぶことにします。この時、付加価値は次のようになります。
付加価値=(粗利潤率+純間接税率)×
生産者価格×実質国内生産額+雇用者所得
粗利潤率=粗利潤/名目国内生産額
純間接税率=純間接税/名目国内生産額
名目国内生産額
=生産者価格×実質国内生産額
産業別の付加価値を記号で示すと以下の通りです。
VA1=(pror1+intaxr1)* P1X1+WEM1
VA2=(pror2+intaxr2) *P2X2+WEM2
VA3= (pror3+ intaxr3) *P3X3+WEM3
prori : i産業の粗利潤率
intaxri : i産業の純間接税率
WEMi:i産業における雇用者所得
雇用者所得は賃金×雇用量であるから
WEMi=Wi×EMi と表記できる
Wi:i産業の賃金
EMi:i産業の雇用量
上式において、WEMiを「Wi×EMi」に置き換えて、それぞれの式について順番に両辺を、X1 、X2、 X3で割ると次のようになります。
VA1/X1
=(pror1+intaxr1)* P1+W1*(EM1/X1)
VA2/X2
=(pror2+intaxr2) * P2+W2*(EM2/X2)
VA3/X3
= (pror3+intaxr3) *P3+W3*(EM3/X3)
これらの式から、各産業の単位当たり付加価値コストは、各産業における粗利潤率、純間接税率、生産者価格、賃金、1単位の生産に必要な雇用量を示す「雇用係数(=EMi/Xi)」で決まることがわかります。
企業は利潤行動の一環として粗利潤率については目標設定をするとみなして、外生変数とします。純間接税率は、政府の税制度等改革等によって決まる政策変数ですから、やはり外生変数です。賃金も企業の人事政策や労使交渉や最低賃金政策などによって外生的に決まると仮定します。
雇用係数は、1単位の生産に必要な雇用量ですから労働生産性に類似しています。雇用係数が下落すれば、1単位生産に必要な雇用量が減少しますから、労働生産性は上昇します。雇用係数が上昇すれば逆に労働生産性は下落します。労働生産性は、技術革新や組織改革などのイノベーションによって決まりますから、やはり外生変数とみなします。粗利潤率、純間接税率、賃金、雇用係数を所与とすれば、各産業の単位当たり付加価値コストは、各産業の生産者価格のみに依存するということになります。

生産者価格を決める連立方程式をもとに、外生変数が変化したとき、どのような経済波及メカニズムが生まれるのか、ひとつの事例として、2次産業の賃金が上昇したケースを考えてみます。
2次産業の賃金が上昇すると、2次産業の単位あたり付加価値コストが増加し、2次産業の生産者価格が上昇します。2次産業の生産者価格上昇によって、1次及び3次産業において2次産業からの中間財投入コストが増加するために、1次産業と3次産業の生産者価格が上昇します。1次産業と3次産業の生産者価格上昇によって、2次産業では中間投入コストが増大し、再び生産者価格が上昇して、1次産業および3次産業の生産者価格に波及していきます。このような波及メカニズムが各産業の生産者価格上昇が収束するまで続くことになります。
2次産業で企業が要求する粗利潤率(=pror2)を高めて強気の価格設定をしたとします。この時も2次産業の単位あたり付加価値コストが増加し、上記で示したような波及効果が起こり、各産業の生産者価格が上昇します。
2次産業で雇用係数が下落した場合はどうでしょうか。雇用係数の下落は、1単位の生産に必要な雇用量が少なくなるといくことですから、2次産業で労働生産性が上昇したことを反映します。2次産業では、単位当たり付加価値コストの低下が可能になり、他の条件に変化がないとすれば、2次産業の生産者価格は下落します。それは、1次産業と3次産業の中間投入コストの下落を通じて両産業の生産者価格が下落します。それが2次産業の中間投入コスト下落に波及し、2次産業の生産者価格はさらに下落します。各産業の生産者価格下落が収束するまで波及効果は続くことになります。
産業別の粗利潤率、純間接税率、賃金、雇用係数の変化は多様な波及メカニズムを通じて各産業の生産者価格に影響を与えます。
各産業の生産者価格の変化は、消費者物価指数にどのように反映するのでしょうか。
各産業で生産される財・サービスに対して家計消費支出が行われますが、家計消費支出全体に占める各産業の財・サービスに対する消費支出の割合をもとめることができます。産業別家計消費支出割合で各産業の生産者価格をウエイトづけすることによって、家計消費出デフレーターがもとまり、これを消費者物価指数とみなすことができます。

(注1)前回の投稿「1. (6) 産業連関表において産業別の生産額はどのように決まり、国民経済レベルのGDPとどのように関係するのでしょうか。」を参照。

