伝統的な産業連関分析は、ケインズの「有効需要の原理」を産業レベルに応用したものです。ケインズが分析対象とした有効需要はいうまでもなくGDPです(以下、「GDP」は全て実質GDPを意味します)。GDPは原材料等の中間財投入の部分を生産額(=販売額)から引いたものを集計したものですから、中間財投入の存在を捨象しています。
しかし、一国経済の活動の様子をきちんと把握するためには、投入される中間財の取引実態をとらえておく必要があります。中間財の取引は、産業間の取引と見なすことができますから、産業と産業の連関関係が重要になります。産業連関表では、産業間の中間財の取引関係を含んだ各産業の生産額が数字的に示されています(=各産業の生産額を産業連関表では「国内生産額」と呼びます)。果たして、産業連関表ではどのようにして産業別の国内生産額をもとめるのでしょうか。今回は、産業連関表をもとに、産業別の国内生産額がどのように決まり、産業別国内生産額と国民経済レベルのGDPはどのように関係するかを論じます。
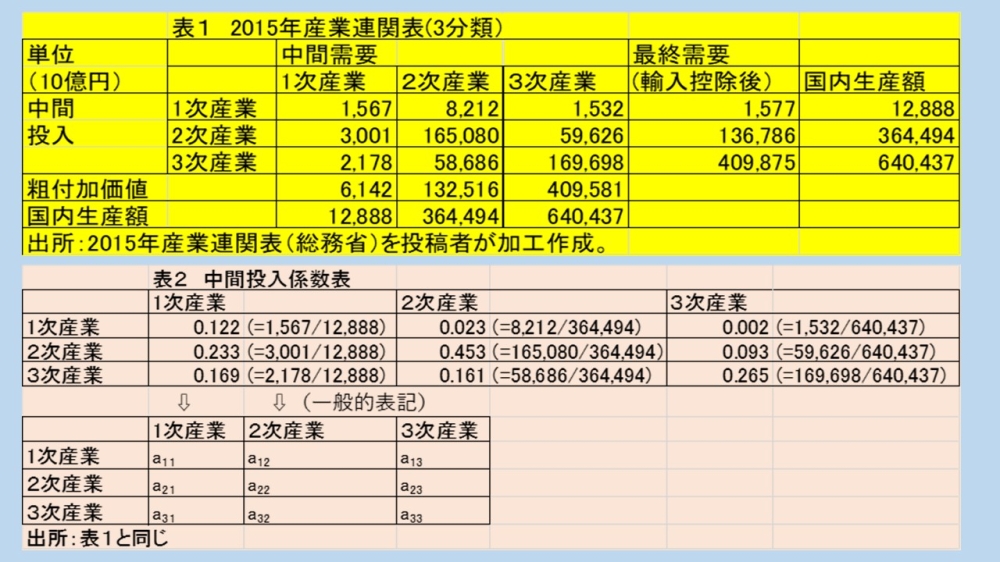
表1は、2015年に作成された産業連関表を、第1次産業、第2次産業、第3次産業の3産業に集計したものです。
表1を行(=横)にそってみると、3つの産業で生産された財・サービスがどのように使われたかという販路構成を示しています。各産業は自らの生産に必要な原材料などの中間財として購入しますが、これが中間需要を生み出します。生産の目的はあくまで最終財にあるので、最終財がどの程度購入されたかを示すのが最終需要です。行は、中間需要と最終需要を合計した需要に対応した生産額が供給されていることを意味します。行は、需要サイドの取引状況を示しているといっていいでしょう。
第1次産業で生産された財・サービスのうち、中間需要として、第1次産業自身が1兆5670億円、第2次産業が8兆2120億円、第3次産業が1兆5320億円購入し、最終需要(輸入控除後)として1兆5770億円が購入され、合計して12兆8880億円の需要に対応して生産されていることがわかります。同様に、第2次産業、第3次産業でも、3産業の中間需要と最終需要(輸入控除後)を合計した需要に対応して、それぞれ364兆4940億円、640兆4370億円の生産が行われたことがわかります。
ここで、最終需要(輸入控除後)について説明します。最終需要は、産業間の取引に影響されず、各経済主体が、最終的に購入する消費・投資・輸出などの需要を示します。消費は家計消費支出、政府消費支出などであり、投資は民間設備投資、民間住宅投資、公的固定資本形成などです。消費や投資は国内の各経済主体の需要ですから、国内最終需要と呼びます。
輸出は外国からの最終需要で、輸出が増えれば、最終需要が増加し、国内の生産は増えます。他方、輸入は海外の財・サービスに対する国内の最終需要であり、輸入が増加すれば、その分国内の需要が海外に漏れることになり、国内の生産は減ることになります。国内最終需要と輸出を合計し、そこから輸入を引いたものを「輸入控除後の最終需要」です。
列は、各産業が財・サービスの生産に必要な原材料などの中間財をどの程度投入したかを示す中間投入と、生産要素である労働や資本の投入によって新たに生み出された付加価値から構成されます。列のデータは、中間投入と付加価値に要した費用を意味するので、列は費用構成になります。別の言い方をすれば、中間財及び労働や資本が生産のためどの程度投入されたかという投入構造(=あるいは生産構造)を示していますので、列は供給サイドを意味することになります。
第1次産業では、12兆8880億円の生産のために、3つの産業から原材料として、それぞれ1兆5670億円分、3兆10億円分、2兆1780億円分の中間財を投入するとともに、6兆1420億円の労働や資本を投入していることがわかります。同様に、第2次産業と第3次産業でも3産業から中間財を調達し、付加価値のもとになる労働や資本を投入して、それぞれ364兆4940億円、640兆4370億円の生産を行ったことがわかります。
産業連関表にはもっとも重要な経済用語のひとつとして中間投入係数があります。中間投入係数とは、各産業の列の中間投入に注目して、中間財の投入額を当該部門の国内生産額で除してもとめた係数のことです。例えば、第1次産業の列に注目すると、第1次産業・第2次産業・第3次産業の中間投入係数はそれぞれ0.122(=1567/12888) 、0.233(=3001/12888)、0.169(=2167/12888)となります。
各産業の中間投入係数を表のかたちでまとめたものが中間投入係数表です。中間投入係数は、一般的に「ai j」 と行列の要素として表記します。この事例では、例えば、a11は0.122、a21は0.2333、a31が0.169、ということになります(表2参照)。
表1から産業連関表を行でみると、産業別に「最終需要(輸入控除後)=国内生産額」という財市場の均衡式が成立しています。表1の財市場均衡式を、中間投入係数を使って修正し、一般的な形で表記すると連立方程式で示すことができます。

産業別財市場均衡式は、各産業に対する中間需要と最終需要(輸入控除後)の合計で産業別需要が決まり、それに等しく各産業は生産を行うことを意味します(=生産した金額が「国内生産額」です)。上記の連立方程式でいうと、第1次・第2次・第3次産業の中間投入係数及び最終需要(輸入控除後)が外生変数として与えられるので、連立方程式を解いて、産業別の国内生産額がもとまり、それらを集計して全体の国内生産額がもとまります。
国内生産額を供給サイドから見ると、中間財や労働・資本を投入して生産が行われ、労働や資本の投入の対価として付加価値が生み出されます。産業連関表からは、産業別に付加価値率(=付加価値/国内生産額)をもとめることができますので、産業別付加価値率に連立方程式を解いて求めた産業別国内生産額を乗じて、産業別付加価値がもとまります。産業別付加価値を集計して国民経済レベルのGDPが決まります。
最終需要(輸入控除後)が産業別国内生産額を決定し、産業別国内生産額から産業別付加価値がもとまり、それを集計して国民経済レベルのGDPが決まるという一連の関係性を確認できました。

