大阪・関西万博は多くの問題を抱えながらも4月13日から始まっています。大阪万博をめぐっては、準備が遅々として進まない状況が続きました。特に、2024年1月1日に能登半島大地震が発生し、多くの建設労働者を復興優先で現地に派遣すべきであるという議論が高まり、一時は万博の中止論や延期論が世論の一つの流れになりました。これに対して、大阪府・市は万博開催の「経済効果」の大きさを強く打ち出し、世界に「大阪」を知ってもらい国際的認知度を高めることの重要性を強調し、予定通り開催し現在に至っています。
最近地方都市では、サッカー・バスケットボールなどの大規模な新しいスタジアム・アリーナが次々に建設されています。例えば、「エディオンピースウイング広島 (広島サッカースタジアム)」は2024年2月に日本初の「まちなかスタジアム」として、原爆ドームのある平和公園近くに建設されました。広島市に限らず、大規模なスタジアム・アリーナの建設は、全国地方都市の大きな流れになっています。
文部科学省管轄のスポーツ庁及び経済産業省は、「スタジアム・アリーナ改革」と称して、「多様な世代が集う交流拠点としてのスタジアム・アリーナ」を2025年までに20拠点を実現するという取り組みを強化しています。スポーツがもたらす新たな交流拠点を、地方都市中心街の再活性化戦略の重要な切り札として位置付けています。
万博に代表されるような大規模イベント開催やスタジアム・アリーナ建設など大型プロジェクトを政策的に推進するために必ず税金という公金が投入されますが、なぜそれが必要かを根拠づける有力な概念が「経済効果」です。イベント開催や施設建設が地域経済に多大な経済効果をもたらすという試算報告書が提出され、それをもとに多額な予算案が当該地方自治体から提案されるのが一般的です。
提案された予算額が地方自治体の政策運営にとって妥当かどうかを評価するためには、その根拠づけになっている「試算された経済効果」を正しく見抜く力が不可欠になります。経済効果の試算は地域別に作成された産業連関表をもとにした産業連関分析という形をとります。ですから、まずは産業連関表とは何かを知ることが経済効果を見抜く力をつけるための第一歩になります。今回の投稿では、産業連関表の見方について簡単に解説します。
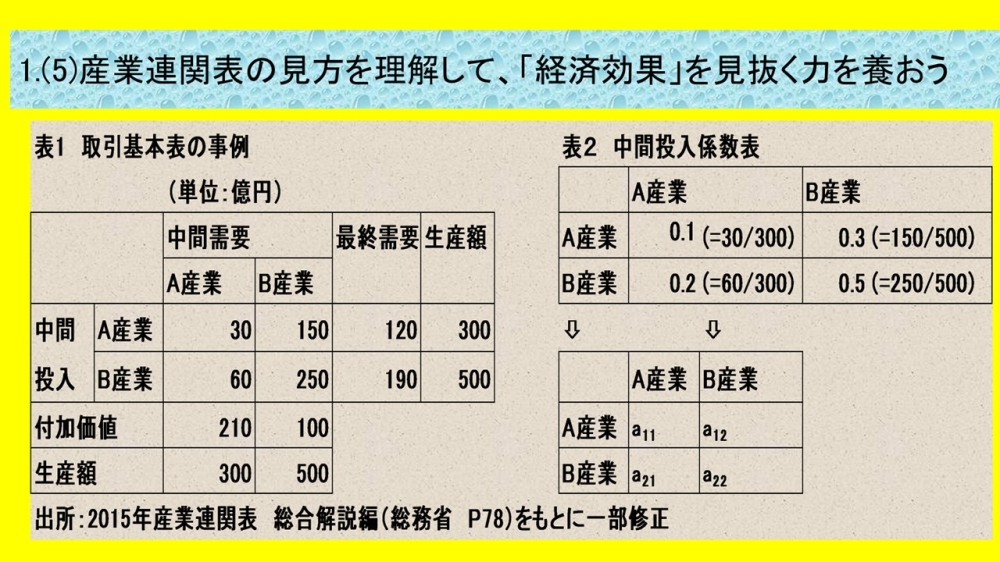
表1は、産業連関表の原型ともいうべき 「取引基本表」の事例です。取引基本表を行(=横)にそってみると、A産業とB産業で生産された財・サービスがどのように使われたかという販路構成を示しています。各産業は生産に必要な原材料などの中間財を購入しますが、これが中間需要を生み出します。生産の目的はあくまで最終財にあるので、最終財がどの程度購入されたかを示すのが最終需要です。行は、中間需要と最終需要を合計した需要に対応した生産額が供給されていることを意味します。行は、需要サイドの取引状況を示しているといっていいでしょう。
表1では、A産業が生産した300億円のうち、中間需要として、A産業自身が30億円、B産業が150億円購入し、最終需要として120億円購入され、合計して300億円の需要に対応していることがわかります。B産業が生産した500億円のうち、中間需要として、A産業が60億円、B産業自身が250億円購入し、最終需要として190億円購入され、合計して500億円の需要に対応していることがわかります。
列(=縦)は、各産業が財・サービスの生産に必要な原材料などの中間財をどの程度投入したかを示す中間投入と、生産要素である労働や資本の投入によって新たに生み出された付加価値から構成されます。列のデータは、中間投入と付加価値に要した費用を意味するので、費用構成になります。別の言い方をすれば、中間財及び労働や資本が生産のためどの程度投入されたかという投入構造(=あるいは生産構造)を示していますので、列は供給サイドを意味することになります。
A産業では、300億円の生産のために、A産業自身とB産業から、それぞれ30億円分、60億円分の中間財を投入するとともに、210億円分の労働や資本を投入して同額の付加価値を生み出していることがわかります。B産業では、500億円の生産のために、A産業とB産業自身から、それぞれ150億円分、250億円分の中間財を投入するとともに、100億円分の労働や資本を投入して同額の付加価値をうみだしています。
産業連関表でもっとも重要な経済用語のひとつが中間投入係数です。中間投入係数とは、「表1 取引基本表の事例」における列に注目して、中間財の投入額を当該部門の生産額で除してもとめた係数のことです。例えば、A産業は、300億円の生産のために、中間財としてA産業自身から30億円、B産業から60億円投入していますから、中間投入係数はそれぞれ0.1(=30/300)、0.2(=60/300)となります。B産業は、500億円の生産のために、中間財をA産業から150億円、B産業自身から250億円を投入していますから、中間投入係数はそれぞれ0.3(=150/500) 、0.5(=250/500)となります。
中間投入係数を表のかたちでまとめたものが中間投入係数表です(表2参照)。
中間投入係数は、一般的に「aij」 と行列の要素として表記します。この事例では、a11 は0.1(=30/300) 、a21は0.2(=60/300)、a12が0.3(=150/500) 、a22が0.5(=250/500)ということになります。
産業連関表では、行が需要サイドを、列が供給サイドを示し、産業ごとに「需要=供給」が成立します。需要と供給が均衡することから、産業別に財市場の均衡式が成立します。表1の事例では、2本の均衡式が成立します。これらの均衡式は、最終的には連立方程式で表記されます。その変形過程を確認して下さい。
30+150+120=300
60+250+190=500
⇩
(30/300) ×300+(150/500) ×500+120=300
(60/300) ×300+(250/500) ×500+190=500
⇩
0.1×300+0.3×500+120=300
0.2×300+0.5×500+190=500
⇩
a11*X1+ a12*X2+F1=X1
a21*X1+ a22*X2+F2=X2
X1 :A産業の生産額 X2:B産業の生産額
F1 :A産業の最終需要 F2:B産業の最終需要
ここで最終需要(F1とF2)が所与であれば、連立方程式を解いて各産業の生産額が決まります。最終需要は、経済主体である家計、企業、政府などが消費や投資などの形で購入する財・サービスの需要を示します。
もし、新たなサッカースタジアムを建設し、そこで定期的試合や様々なイベントが開催された場合、建設のための投資額や観客数の見通しが生み出す消費額などを試算して、最終需要として与えると、当該地域の各産業の生産額にどの程度波及効果をもたらすか知ることができます。
このように、地域別の産業連関表が作成されていれば、それをもとに評価したい新規プロジェクトの経済効果を計算することが可能になります。「経済効果」を見抜く力の第一歩は、産業連関表の全体像の理解にあることを強調したいと思います。

